ボツリヌス膀胱注射
年間300件以上のBOTOX膀胱注射治療をしている当院にとって、科学的に最適な治療を考えることは至上命題です。
今回は数学を使って、その安全な治療法を考えていきます。
離散数学という学問があります。迷路がその代表で、どこへ行けばいいかわからないものです
この迷路が、人間の体だとします。人間の体には、幾つもの要因があります。糖尿病、高血圧、、、、
その他には、頭痛、腰痛、様々です
一般に治療するときは、頻尿のみを見るのですが、それでは不十分になりました
いろんなデータを合わせて、統合します。つまり、迷路から最短で脱出するようものです
![]()
有名な「オイラーの七つの橋の問題」というものがあります。ヴェニスのような街に橋がかかっています。
全ての橋を渡るのですが、その上で最短距離を探さないと行けないというゲームにします
幾つものはしは、全て病気のことです。これらのはしを渡ることで、最終的に目的地にたどり着きます。
今回の研究は、このような遊びの数学をとりいれます。
膀胱注射をする患者さんの持つ様々な病気を計算の上で、離散数学で最適な最短距離を計算するのです。
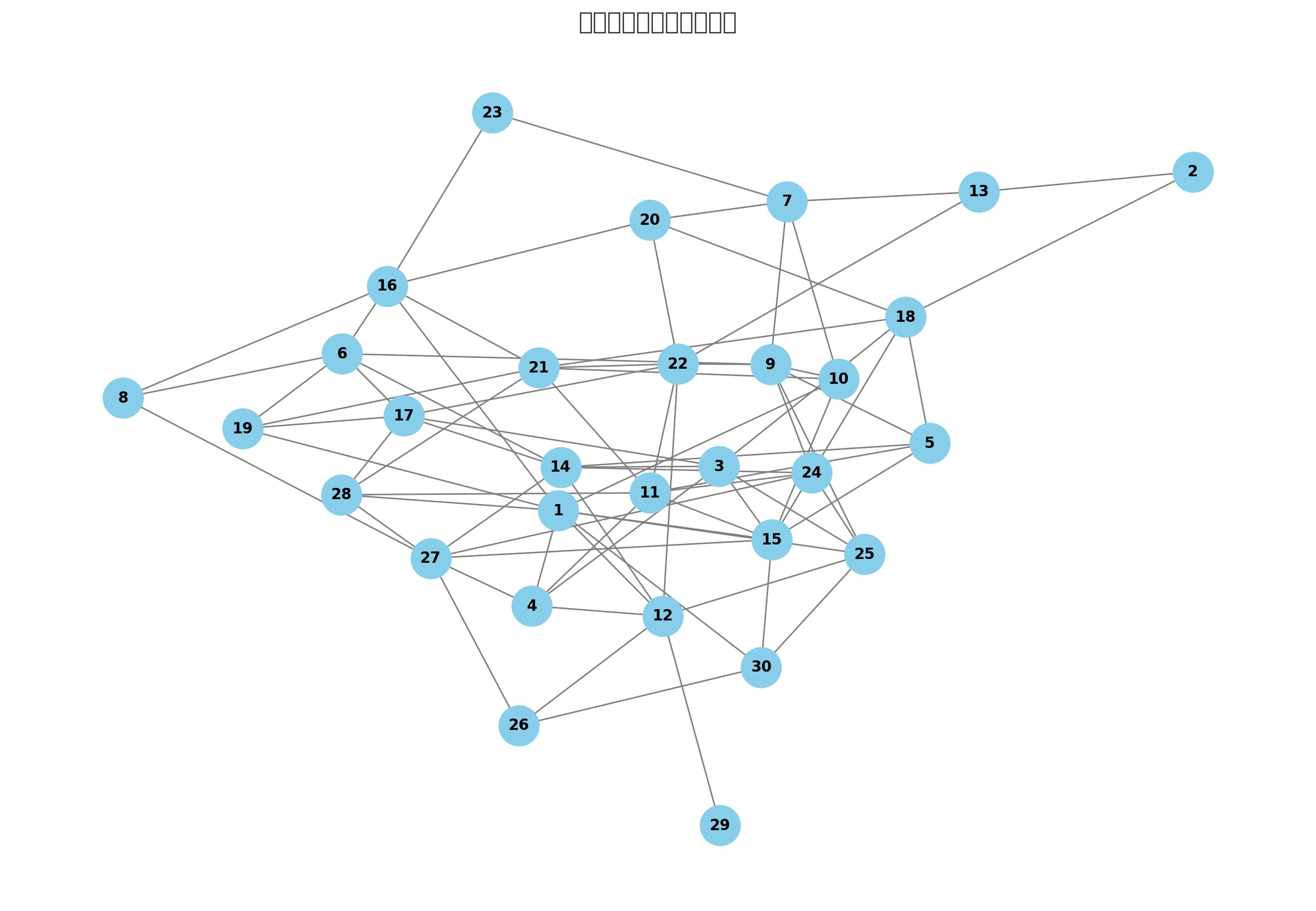
このように様々な要因を用意します。このうち、BOTOX治療は、①です。たとえば、30からいく最短きょりはわかりますか?
このように臨床医学は、単純ではなく、多くの病気を計算する数学が必要なのです。
論文を読んでみますか?
Innovative decision making tools using discrete mathematics for stress urinary incontinence treatment.
Okui N.
Sci Rep. 2024 Apr 30;14(1):9900. doi: 10.1038/s41598-024-60407-w.
A Discrete Mathematics Approach for Understanding Risk Factors in Overactive Bladder Treatment.
Okui N.
Cureus. 2024 Jan 30;16(1):e53245. doi: 10.7759/cureus.53245. eCollection 2024 Jan.
合わせて読みたい